選択した画像 sum of 1/n^2 formula 109622-Sum of series 1+2+3+4+....+n formula

 The way the items are ordered now you can see that each of those pairs is equal to N (N11 is N, N22 is N) Since there are N1 items, there are (N1)/2 such pairs So you're adding N (N1)/2 times, so the total value is N*(N1)/2

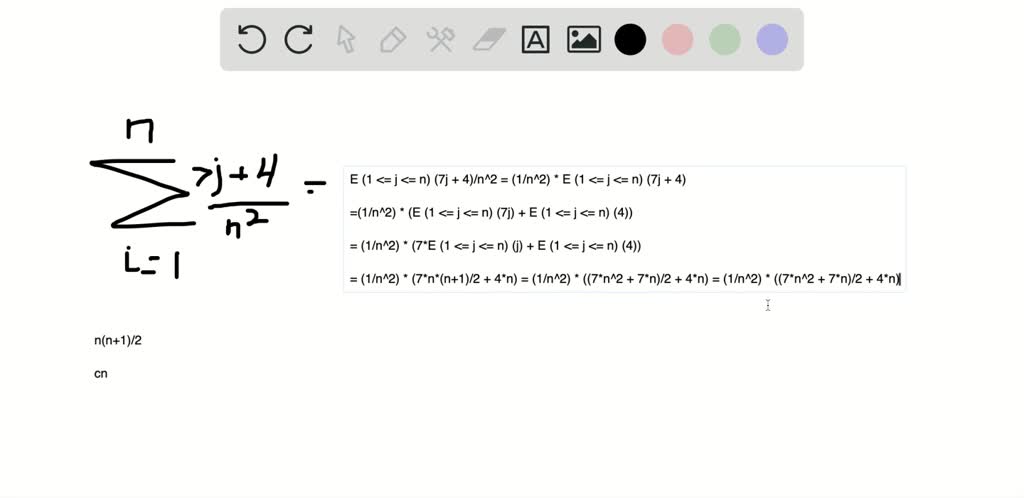
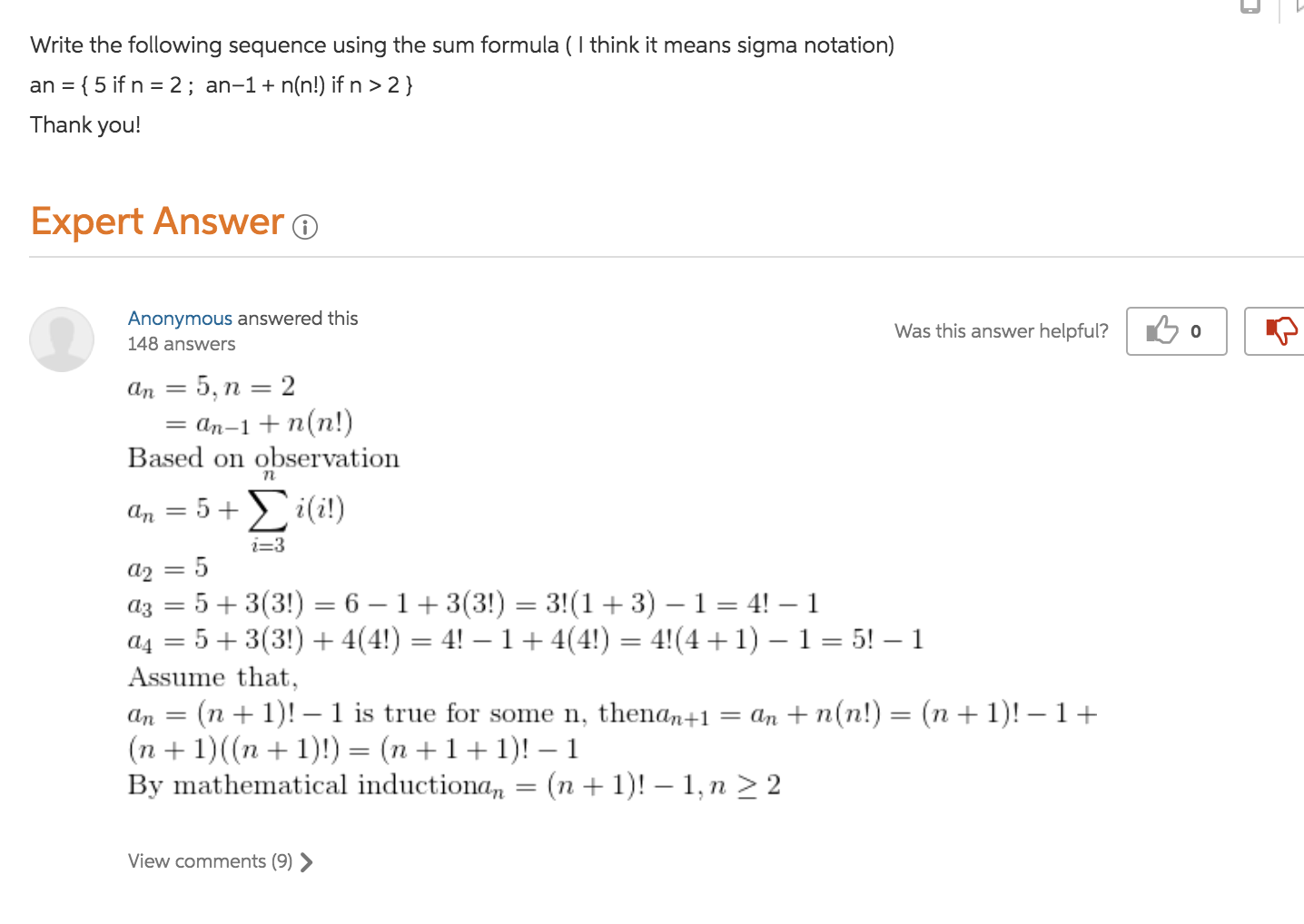
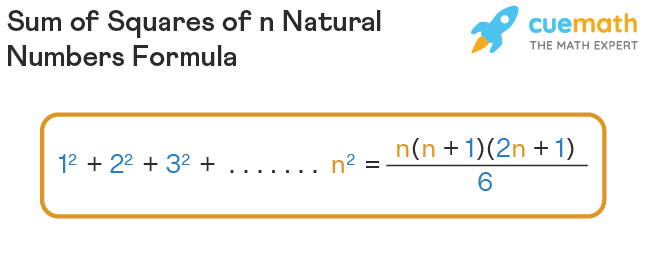
Sum of series 1+2+3+4+....+n formula-The sum of the powers of two is one less than the product of the next power Don't take my word for it Try it with a larger valueFormula for the sum 1 2 2 2 3 2

Sum of series 1+2+3+4+....+n formulaのギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Sum of series 1+2+3+4+....+n formula」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Sum of series 1+2+3+4+....+n formula」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Sum of series 1+2+3+4+....+n formula」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Sum of series 1+2+3+4+....+n formula」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Sum of series 1+2+3+4+....+n formula」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Sum of series 1+2+3+4+....+n formula」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Sum of series 1+2+3+4+....+n formula」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

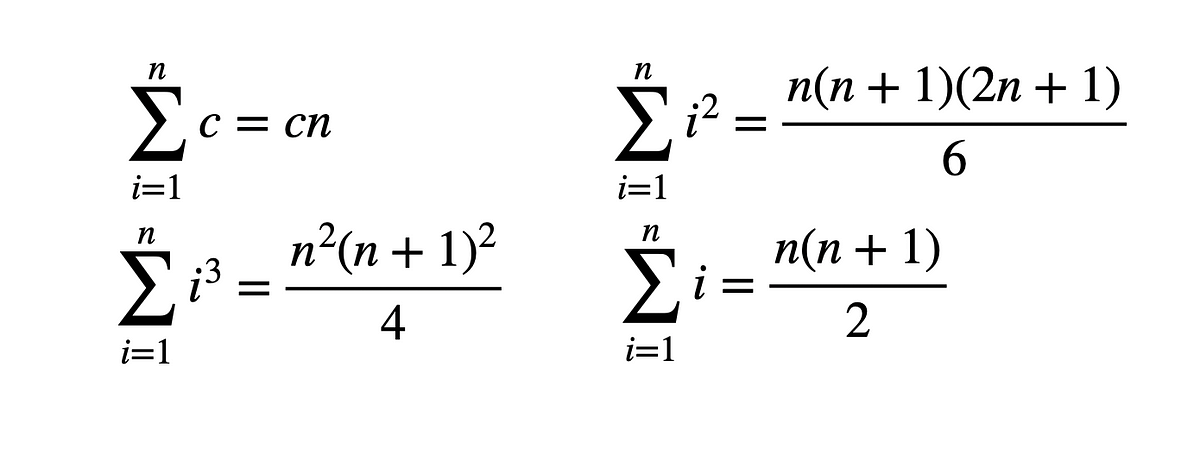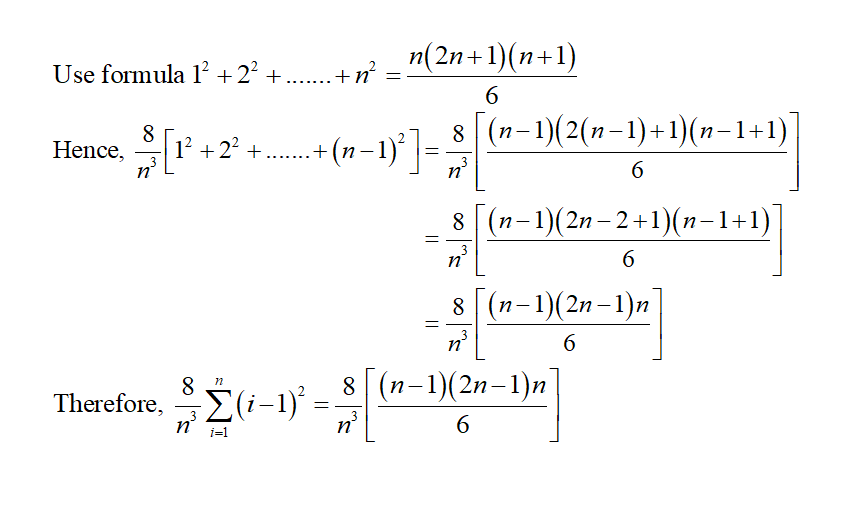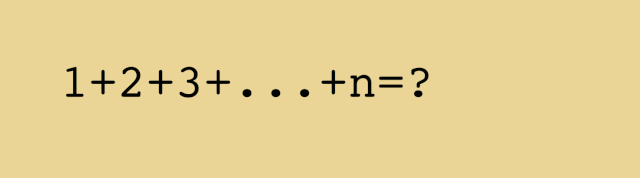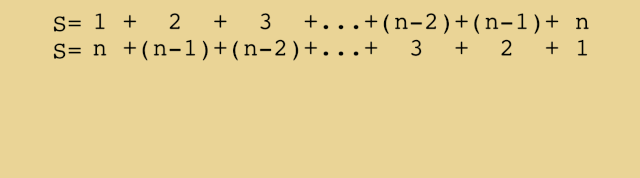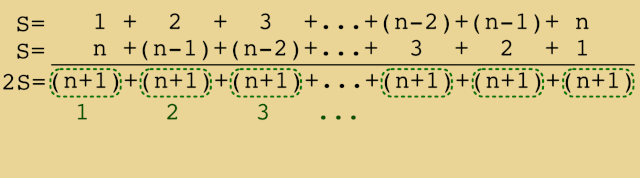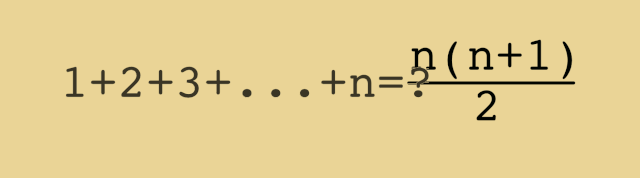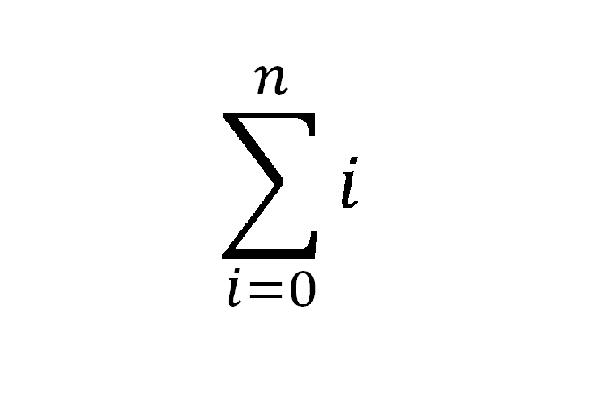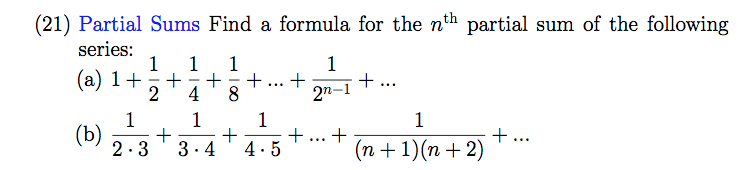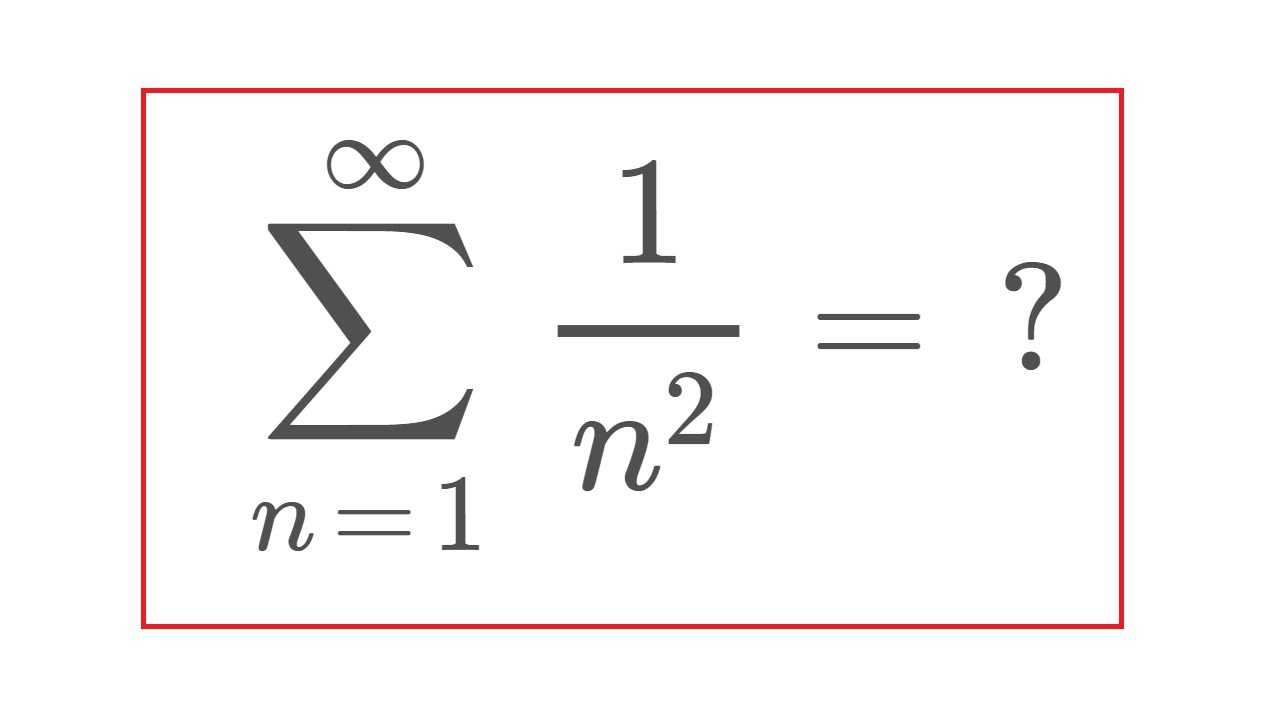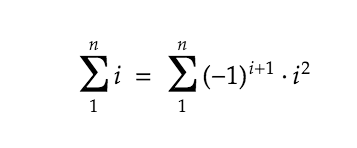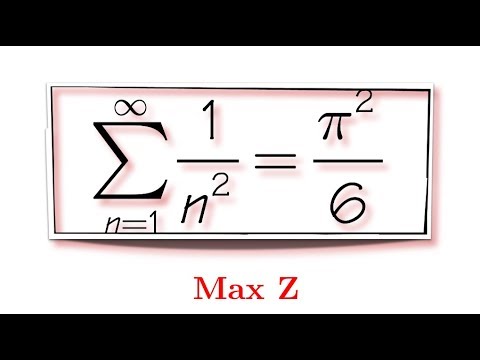「Sum of series 1+2+3+4+....+n formula」の画像ギャラリー、詳細は各画像をクリックしてください。

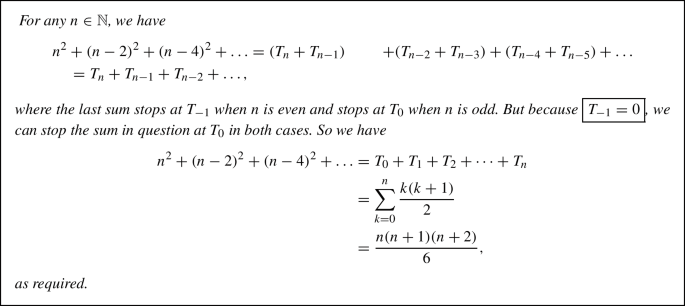Contact Pro Premium Expert Support »Reading time 30 minutes Coding time 2 minutes In this problem, we will find the sum of the first N integers that is 1 to N In the brute force approach, we need to add each number which will take linear time O(N) but we can solve this in constant time O(1) by using an insightful formula

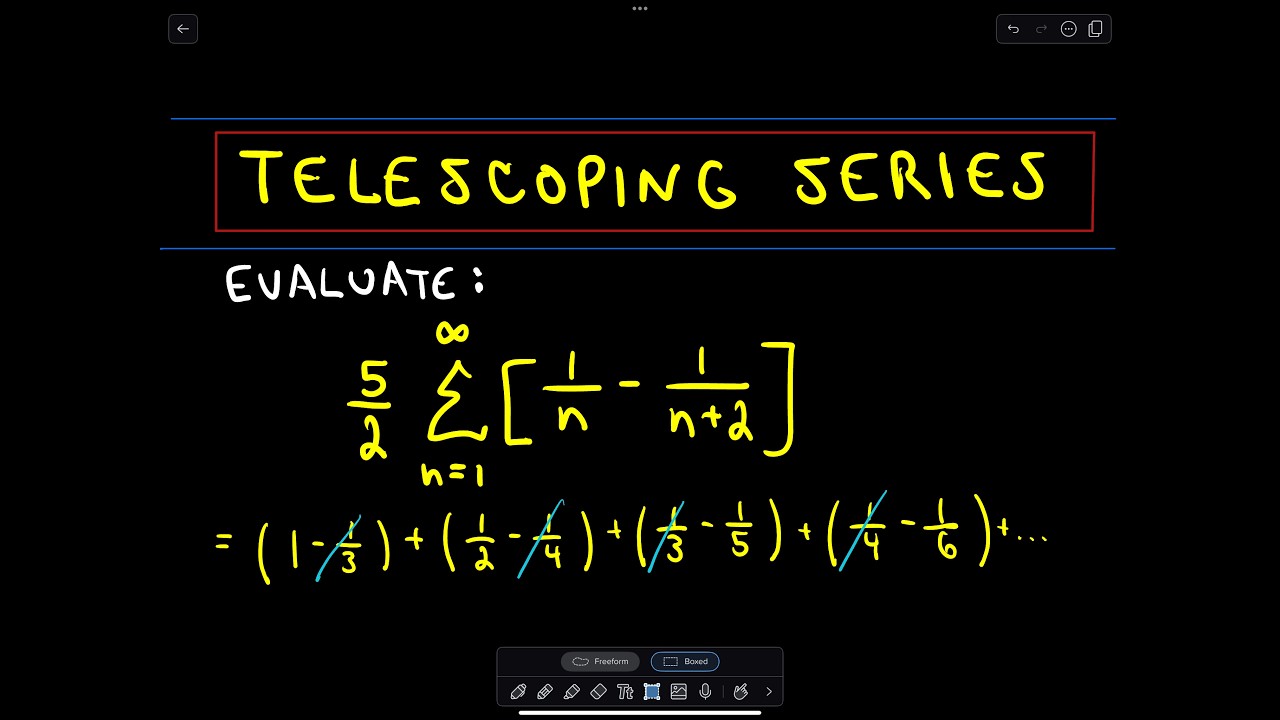
Incoming Term: sum of 1/n^2 formula, sum of 1+2+3+...+n formula, sum of series 1+2+3+4+....+n formula, sum of 1 + 2 + 3 upto n formula, sum of series formula 1+2+3+...+n,